Úloha 4.3

Napíšte program, zdrojový kód, v jazyku C++ použitím štandardu C++17, ktorý realizuje nasledovnú činnosť.

Implementujte graf, ktorého hrany majú definovanú váhu, t.j. ováhovaný graf. Uzol grafu má označenie ‘label’ typu string. Hrana spájajúca dva uzly musí mať definovanú váhu typu int. Hrany medzi uzlami nemajú orientáciu a tak prechádzanie medzi uzlami môže byť oboma smermi.

Pre graf implementujte nasledovné metódy:

bool add_vertex(Vertex*, int*) - Pridanie nového uzla do grafu. Metóda má byť ako public člen triedy Vertex. Prvý argument je pointer na uzol s ktorým chceme prepojenie vytvoriť. Druhý argument je váha hrany, ktorá bude vytvorená medzi týmito dvomi uzlami.
int count(vector<string>*) - Ak váha hrany predstavuje cenu, ktorú treba zaplatiť aby sme prešli po danej hrane na ďalší uzol, tak táto metóda vráti celkovú cenu cesty z uzla na uzol. Argument metódy je cesta prechádzania uzlov, kde prvok vektora je označenie (label) uzla. Ak taká cesta v grafe existuje metóda vráti jej celkovú cenu. Ak cesta neexistuje, t.j. neexistuje hrana, ktorá by prepojila dva uzly, ktoré sú za sebou definové vo vstupnom vektore, metóda vráti hodnotu -1.

Príklady vstupov / výstupov programu

Ak máme graf s nasledujúcou štruktúrou:

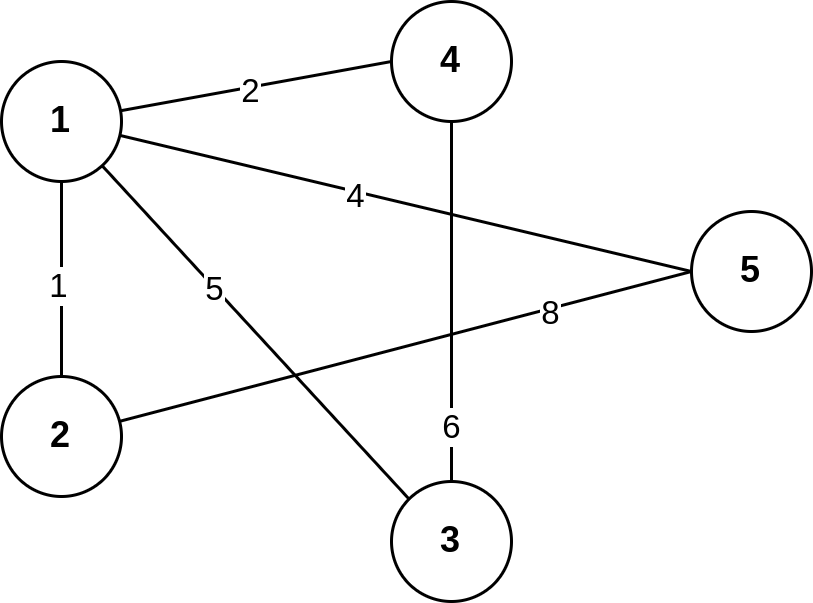
graph

Volanie funkcie pre výpočet celkovej ceny cesty (celkovej váhy) má nasledovné výsledky:

count({1,4,3}) == 8;
count({2,5,1,4}) == 14;
count({3,1,2,5,1}) == 18;

Rozbaľ pre ukážku riešenia

Ováhovaný neorientovaný graf implementovaný pomocou triedy Vertex. Každý vrchol uchováva informácie o svojich susedoch a váhach hrán.

#include <iostream>
#include <unordered_map>
#include <vector>
#include <string>

using namespace std;

class Vertex {
private:
    string label;
    unordered_map<string, pair<Vertex*, int>> neighbors; // mapa: label suseda -> (pointer, váha)

public:
    // Konštruktor
    explicit Vertex(const string& lbl) : label(lbl) {}

    // Getter pre label
    string get_label() const {
        return label;
    }

    // Pridanie hrany medzi this a druhým uzlom
    bool add_vertex(Vertex* other, int* weight_ptr) {
        if (!other || !weight_ptr) return false;

        const string& other_label = other->get_label();

        // Ak už je hrana medzi týmito uzlami, nepridávaj znova
        if (neighbors.find(other_label) != neighbors.end()) {
            return false;
        }

        // Pridaj hranu do oboch strán (graf je neorientovaný)
        neighbors[other_label] = make_pair(other, *weight_ptr);
        other->neighbors[label] = make_pair(this, *weight_ptr);

        return true;
    }

    // Spočítanie ceny cesty podľa zoznamu labelov
    int count(vector<string>* path) {
        if (!path || path->empty()) return -1;

        int total_cost = 0;
        Vertex* current = this;

        for (size_t i = 1; i < path->size(); ++i) {
            const string& next_label = (*path)[i];

            auto it = current->neighbors.find(next_label);
            if (it == current->neighbors.end()) {
                return -1; // neexistuje hrana medzi current a next_label
            }

            total_cost += it->second.second; // pripočítaj váhu hrany
            current = it->second.first;      // posuň sa na ďalší uzol
        }

        return total_cost;
    }
};

int main() {
    // Vytvorenie vrcholov
    Vertex a("A");
    Vertex b("B");
    Vertex c("C");
    Vertex d("D");

    // Vytvorenie hrán s váhami
    int ab = 5;
    int ac = 3;
    int bc = 2;
    int cd = 4;

    a.add_vertex(&b, &ab);
    a.add_vertex(&c, &ac);
    b.add_vertex(&c, &bc);
    c.add_vertex(&d, &cd);

    // Cesta: A -> C -> D
    vector<string> path1 = {"A", "C", "D"};
    cout << "Cost A->C->D: " << a.count(&path1) << endl; // očakávané: 3 + 4 = 7

    // Cesta: A -> B -> C -> D
    vector<string> path2 = {"A", "B", "C", "D"};
    cout << "Cost A->B->C->D: " << a.count(&path2) << endl; // očakávané: 5 + 2 + 4 = 11

    // Neexistujúca cesta: A -> D
    vector<string> path3 = {"A", "D"};
    cout << "Cost A->D: " << a.count(&path3) << endl; // očakávané: -1

    return 0;
}

Vysvetlenie

Každý Vertex obsahuje mapu svojich susedov (unordered_map<string, pair<Vertex*, int>>), kde:
- string je label suseda,
- Vertex* je pointer na suseda,
- int je váha hrany.
Metóda add_vertex() zabezpečuje pridanie obojstrannej hrany (graf je neorientovaný).
Metóda count() počíta cenu cesty cez daný zoznam názvov uzlov – ak niektorá hrana chýba, vráti -1.

Ukážkový výstup

Cost A->C->D: 7
Cost A->B->C->D: 11
Cost A->D: -1

ASCII vizualizácia

     [A]
     / \
  5 /   \ 3
   /     \
 [B]--2--[C]--4--[D]

Úloha 4.2